Proof
VIDEO COMING SOON…
In this post we’re going to be looking at Proofs.
Proof questions can come in all shapes and sizes. You may be asked to prove something in terms of Algebra (Algebraic proof), disprove a comment made by someone (Proof by counter example), prove a certain set of angles equals a given number of degrees (Geometric proof) and even proof the difference between a set of 2 indices is a multiple of another number (Proof with indicies).
Now this is a lot to take in at once so we’re going to go over each proof individually and do some worked examples for each – but first there are 3 extremely important rules you need to remember:
- We represent a number in a formula using \(n\) – even numbers are therefore expressed as \(2n\) and odd number are expressed as \(2n+1\).
- Consecutive numbers are written as \(n, n+1,n+2\), etc.
- \(Odd \times Odd = Odd\), \(Even \times Even = Even\) and \(Odd \times Even = Even.\)
Algebraic proof
So let’s look at Algebraic proof first. For this, we essentially need to create an algebraic expression that matches what our question is asking, then, using the forumla, prove whatever the question is asking us to prove.
A quick and easy example of this would be something like: ‘Prove that the sum of 2 consecutive numbers is always odd’.
Now we know from our ‘3 extremely important rules’ that even numbers will always be expressed as \(2n\) and odd numbers will always be expressed as \(2n+1\).
Baring this in mind, we now need to write out a formula that represents the sum of 2 consecutive numbers → if we represent a number as \(n\), our next number will be \(n+1\). So the sum of 2 consecutive numbers can be expressed as \(n+n+1\).
If we collect our terms, we are left with \(2n+1\) which is what we said will always represent an odd number → there’s our proof!
Disprove by counter example
This type of proof is what it says on the tin – we to disprove a statement made by giving an example that undermines the statement. Questions on this will include something along the lines of ‘prove why this statement is wrong’.
Let’s look at an example of this:
Prove or disprove the statement that all prime numbers are odd.
This one doesn’t actually need any algebra – you can simply state that a prime number is any number that can only be divided by itself and 1. 2 can only be divided by itself and 1 and is, therefore, a prime number. 2 is also even. Therefore the statement that all prime numbers are odd is incorrect.
So so simple.
Geometric proof
Geometric proof is similar to Algebraic proof, however instead of proving something around numbers and unknowns – we are looking at proving fundamentals of shapes.
A great example of geometric proof questions would be ‘prove that the interior angles of a triangle add up to 180 degrees’ – we need to use a diagram to show this:
- Sketch out a diagram of a triangle – label each of the angles; this could be \(x, y, z\) or \(a, b, c\) – it doesn’t make a difference & add a straight line parallel to the bottom of the triangle, that touches the top angle. Hard to explain using words but here’s an illustration to help:
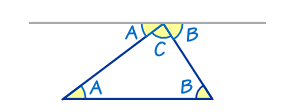
(credit: mathisisfun.com)
- You can now explain using your diagram, why all angles in a triangle add up to 180 degrees.
- Angles A and B in the triangle are ‘Z’ angles which means that Angles A and B on the straight lines are the same.
- When looking at the straight line, we can see that the straight line is the same as the sum of Angles A, B and C.
- We also know that a straight line = 180 degrees and therefore the sum of Angles A, B and C are also 180 degrees.
Proof with indicies
This is another self-explanatory topic but this is proving statements with the use of indices.
A great example of this may be something like ‘Prove that the difference between \(24^{12}\) and \(15^{10}\) is a multiple of 3’ – (credit: MathsMadeEasy)
The goal of questions like these are to re-write this question in the form of an equation that includes the number 3 factored outside of brackets (therefore we know it will definitely be a factor of 3) – you would do the following:
- Write out the question as an expression: \(24^{12}-15^{10}\).
- Rewrite the expression, splitting out a number from each of the indicies – like so: \((24 \times 24^{11}) – (15 \times 15^{9})\)
- Then breakdown our single number into its factors, ensuring both brackets will have a number in common: \((3\times8\times24^{11})-(3\times5\times15^9)\)
- We can now factor the 3 from each side to leave us with \(3([8\times24^{11}]-[5\times15^9])\)
- Based on the above, we have proven that the difference between \(24^{12}\) and \(15^{10}\) is a multiple of 3.
Hopefully this all made sense. If you have any questions on this, please leave them in the comments and I’ll get back to you as soon as I can.
Once you’re happy with the above, please give the Question Practice section a go to make sure you’re ready for this to come up in the exam!